Note
Go to the end to download the full example code.
Custom Operator for NMF Decomposition¶
NMF factorizes an input matrix into two matrices W, H of rank k so that \(WH \sim M`\). \(M=(m_{ij})\) may be a binary matrix where i is a user and j a product he bought. The prediction function depends on whether or not the user needs a recommandation for an existing user or a new user. This example addresses the first case.
The second case is more complex as it theoretically requires the estimation of a new matrix W with a gradient descent.
Building a simple model¶
import os
import skl2onnx
import onnxruntime
import sklearn
from sklearn.decomposition import NMF
import numpy as np
import matplotlib.pyplot as plt
from onnx.tools.net_drawer import GetPydotGraph, GetOpNodeProducer
import onnx
from skl2onnx.algebra.onnx_ops import OnnxArrayFeatureExtractor, OnnxMul, OnnxReduceSum
from skl2onnx.common.data_types import FloatTensorType
from onnxruntime import InferenceSession
mat = np.array(
[[1, 0, 0, 0], [1, 0, 0, 0], [1, 0, 0, 0], [1, 0, 0, 0], [1, 0, 0, 0]],
dtype=np.float64,
)
mat[: mat.shape[1], :] += np.identity(mat.shape[1])
mod = NMF(n_components=2)
W = mod.fit_transform(mat)
H = mod.components_
pred = mod.inverse_transform(W)
print("original predictions")
exp = []
for i in range(mat.shape[0]):
for j in range(mat.shape[1]):
exp.append((i, j, pred[i, j]))
print(exp)
original predictions
[(0, 0, np.float64(1.8940570076830285)), (0, 1, np.float64(0.3072441822407282)), (0, 2, np.float64(0.10911047375804805)), (0, 3, np.float64(0.3072441822407282)), (1, 0, np.float64(1.1066071879294734)), (1, 1, np.float64(0.19083385427868077)), (1, 2, np.float64(0.0)), (1, 3, np.float64(0.19083385427868077)), (2, 0, np.float64(1.0146710371562229)), (2, 1, np.float64(0.0)), (2, 2, np.float64(0.9848903284716739)), (2, 3, np.float64(0.0)), (3, 0, np.float64(1.1066071879294734)), (3, 1, np.float64(0.19083385427868077)), (3, 2, np.float64(0.0)), (3, 3, np.float64(0.19083385427868077)), (4, 0, np.float64(0.9470285038415143)), (4, 1, np.float64(0.1536220911203641)), (4, 2, np.float64(0.05455523687902403)), (4, 3, np.float64(0.1536220911203641))]
Let’s rewrite the prediction in a way it is closer to the function we need to convert into ONNX.
[(0, 0, np.float64(1.8940570076830285)), (0, 1, np.float64(0.3072441822407282)), (0, 2, np.float64(0.10911047375804805)), (0, 3, np.float64(0.3072441822407282)), (1, 0, np.float64(1.1066071879294734)), (1, 1, np.float64(0.19083385427868077)), (1, 2, np.float64(0.0)), (1, 3, np.float64(0.19083385427868077)), (2, 0, np.float64(1.0146710371562229)), (2, 1, np.float64(0.0)), (2, 2, np.float64(0.9848903284716739)), (2, 3, np.float64(0.0)), (3, 0, np.float64(1.1066071879294734)), (3, 1, np.float64(0.19083385427868077)), (3, 2, np.float64(0.0)), (3, 3, np.float64(0.19083385427868077)), (4, 0, np.float64(0.9470285038415143)), (4, 1, np.float64(0.1536220911203641)), (4, 2, np.float64(0.05455523687902403)), (4, 3, np.float64(0.1536220911203641))]
Conversion into ONNX¶
There is no implemented converter for NMF as the function we plan to convert is not transformer or a predictor. The following converter does not need to be registered, it just creates an ONNX graph equivalent to function predict implemented above.
def nmf_to_onnx(W, H, op_version=12):
"""
The function converts a NMF described by matrices
*W*, *H* (*WH* approximate training data *M*).
into a function which takes two indices *(i, j)*
and returns the predictions for it. It assumes
these indices applies on the training data.
"""
col = OnnxArrayFeatureExtractor(H, "col")
row = OnnxArrayFeatureExtractor(W.T, "row")
dot = OnnxMul(col, row, op_version=op_version)
res = OnnxReduceSum(dot, output_names="rec", op_version=op_version)
indices_type = np.array([0], dtype=np.int64)
onx = res.to_onnx(
inputs={"col": indices_type, "row": indices_type},
outputs=[("rec", FloatTensorType((None, 1)))],
target_opset=op_version,
)
return onx
model_onnx = nmf_to_onnx(W.astype(np.float32), H.astype(np.float32))
print(model_onnx)
ir_version: 7
producer_name: "skl2onnx"
producer_version: "1.20.0"
domain: "ai.onnx"
model_version: 0
graph {
node {
input: "Ar_ArrayFeatureExtractorcst"
input: "col"
output: "Ar_Z0"
name: "Ar_ArrayFeatureExtractor"
op_type: "ArrayFeatureExtractor"
domain: "ai.onnx.ml"
}
node {
input: "Ar_ArrayFeatureExtractorcst1"
input: "row"
output: "Ar_Z02"
name: "Ar_ArrayFeatureExtractor1"
op_type: "ArrayFeatureExtractor"
domain: "ai.onnx.ml"
}
node {
input: "Ar_Z0"
input: "Ar_Z02"
output: "Mu_C0"
name: "Mu_Mul"
op_type: "Mul"
domain: ""
}
node {
input: "Mu_C0"
output: "rec"
name: "Re_ReduceSum"
op_type: "ReduceSum"
domain: ""
}
name: "OnnxReduceSum"
initializer {
dims: 2
dims: 4
data_type: 1
float_data: 1.97894239
float_data: 0.341267616
float_data: 0
float_data: 0.341267616
float_data: 0.896073699
float_data: 0
float_data: 0.869773805
float_data: 0
name: "Ar_ArrayFeatureExtractorcst"
}
initializer {
dims: 2
dims: 5
data_type: 1
float_data: 0.900302768
float_data: 0.559191227
float_data: 0
float_data: 0.559191227
float_data: 0.450151384
float_data: 0.125446945
float_data: 0
float_data: 1.13235223
float_data: 0
float_data: 0.0627234727
name: "Ar_ArrayFeatureExtractorcst1"
}
input {
name: "col"
type {
tensor_type {
elem_type: 7
shape {
dim {
}
}
}
}
}
input {
name: "row"
type {
tensor_type {
elem_type: 7
shape {
dim {
}
}
}
}
}
output {
name: "rec"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
dim_value: 1
}
}
}
}
}
}
opset_import {
domain: ""
version: 12
}
opset_import {
domain: "ai.onnx.ml"
version: 1
}
Let’s compute prediction with it.
sess = InferenceSession(
model_onnx.SerializeToString(), providers=["CPUExecutionProvider"]
)
def predict_onnx(sess, row_indices, col_indices):
res = sess.run(None, {"col": col_indices, "row": row_indices})
return res
onnx_preds = []
for i in range(mat.shape[0]):
for j in range(mat.shape[1]):
row_indices = np.array([i], dtype=np.int64)
col_indices = np.array([j], dtype=np.int64)
pred = predict_onnx(sess, row_indices, col_indices)[0]
onnx_preds.append((i, j, pred[0, 0]))
print(onnx_preds)
[(0, 0, np.float32(1.894057)), (0, 1, np.float32(0.30724418)), (0, 2, np.float32(0.10911047)), (0, 3, np.float32(0.30724418)), (1, 0, np.float32(1.1066072)), (1, 1, np.float32(0.19083385)), (1, 2, np.float32(0.0)), (1, 3, np.float32(0.19083385)), (2, 0, np.float32(1.0146711)), (2, 1, np.float32(0.0)), (2, 2, np.float32(0.9848903)), (2, 3, np.float32(0.0)), (3, 0, np.float32(1.1066072)), (3, 1, np.float32(0.19083385)), (3, 2, np.float32(0.0)), (3, 3, np.float32(0.19083385)), (4, 0, np.float32(0.9470285)), (4, 1, np.float32(0.15362209)), (4, 2, np.float32(0.054555234)), (4, 3, np.float32(0.15362209))]
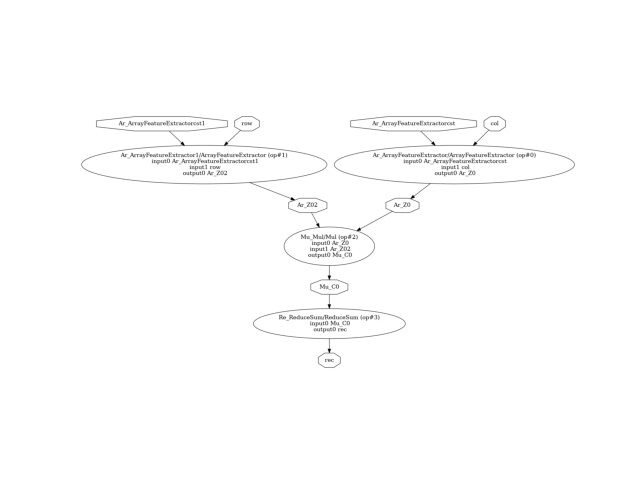
The ONNX graph looks like the following.
pydot_graph = GetPydotGraph(
model_onnx.graph,
name=model_onnx.graph.name,
rankdir="TB",
node_producer=GetOpNodeProducer("docstring"),
)
pydot_graph.write_dot("graph_nmf.dot")
os.system("dot -O -Tpng graph_nmf.dot")
image = plt.imread("graph_nmf.dot.png")
plt.imshow(image)
plt.axis("off")
(np.float64(-0.5), np.float64(1654.5), np.float64(846.5), np.float64(-0.5))
Versions used for this example
print("numpy:", np.__version__)
print("scikit-learn:", sklearn.__version__)
print("onnx: ", onnx.__version__)
print("onnxruntime: ", onnxruntime.__version__)
print("skl2onnx: ", skl2onnx.__version__)
numpy: 2.4.1
scikit-learn: 1.8.0
onnx: 1.21.0
onnxruntime: 1.24.0
skl2onnx: 1.20.0
Total running time of the script: (0 minutes 0.274 seconds)