ONNX with Python¶
Next sections highlight the main functions used to build an ONNX graph with the Python API onnx offers.
A simple example: a linear regression¶
The linear regression is the most simple model
in machine learning described by the following expression
\(Y = XA + B\). We can see it as a function of three
variables \(Y = f(X, A, B)\) decomposed into
y = Add(MatMul(X, A), B). That what’s we need to represent
with ONNX operators. The first thing is to implement a function
with ONNX operators.
ONNX is strongly typed. Shape and type must be defined for both
input and output of the function. That said, we need four functions
to build the graph among the make function:
make_tensor_value_info: declares a variable (input or output) given its shape and typemake_node: creates a node defined by an operation (an operator type), its inputs and outputsmake_graph: a function to create an ONNX graph with the objects created by the two previous functionsmake_model: a last function which merges the graph and additional metadata
All along the creation, we need to give a name to every input, output of every node of the graph. Input and output of the graph are defined by onnx objects, strings are used to refer to intermediate results. This is how it looks like.
# imports
from onnx import TensorProto
from onnx.helper import (
make_model, make_node, make_graph,
make_tensor_value_info)
from onnx.checker import check_model
# inputs
# 'X' is the name, TensorProto.FLOAT the type, [None, None] the shape
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
# outputs, the shape is left undefined
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
# nodes
# It creates a node defined by the operator type MatMul,
# 'X', 'A' are the inputs of the node, 'XA' the output.
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
# from nodes to graph
# the graph is built from the list of nodes, the list of inputs,
# the list of outputs and a name.
graph = make_graph([node1, node2], # nodes
'lr', # a name
[X, A, B], # inputs
[Y]) # outputs
# onnx graph
# there is no metadata in this case.
onnx_model = make_model(graph)
# Let's check the model is consistent,
# this function is described in section
# Checker and Shape Inference.
check_model(onnx_model)
# the work is done, let's display it...
print(onnx_model)
ir_version: 11
graph {
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
}
name: "lr"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
version: 23
}
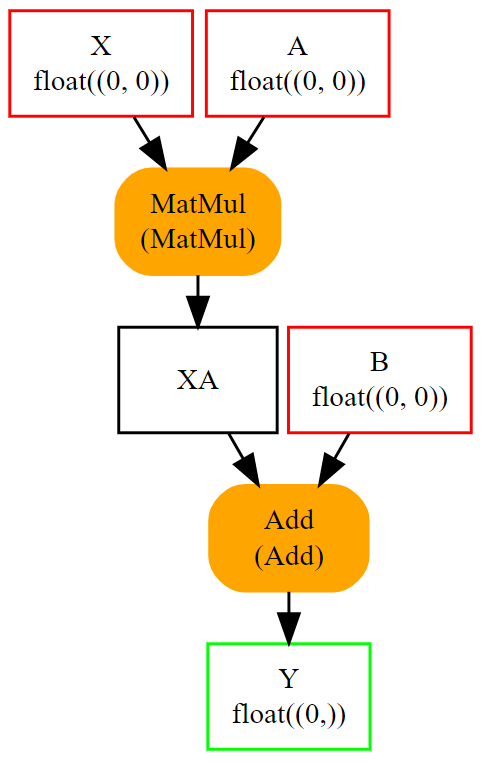
An empty shape (None) means any shape, a shape defined as [None, None]
tells this object is a tensor with two dimensions without any further precision.
The ONNX graph can also be inspected by looking into the fields
of each object of the graph.
from onnx import TensorProto
from onnx.helper import (
make_model, make_node, make_graph,
make_tensor_value_info)
from onnx.checker import check_model
def shape2tuple(shape):
return tuple(getattr(d, 'dim_value', 0) for d in shape.dim)
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
graph = make_graph([node1, node2], 'lr', [X, A, B], [Y])
onnx_model = make_model(graph)
check_model(onnx_model)
# the list of inputs
print('** inputs **')
print(onnx_model.graph.input)
# in a more nicely format
print('** inputs **')
for obj in onnx_model.graph.input:
print("name=%r dtype=%r shape=%r" % (
obj.name, obj.type.tensor_type.elem_type,
shape2tuple(obj.type.tensor_type.shape)))
# the list of outputs
print('** outputs **')
print(onnx_model.graph.output)
# in a more nicely format
print('** outputs **')
for obj in onnx_model.graph.output:
print("name=%r dtype=%r shape=%r" % (
obj.name, obj.type.tensor_type.elem_type,
shape2tuple(obj.type.tensor_type.shape)))
# the list of nodes
print('** nodes **')
print(onnx_model.graph.node)
# in a more nicely format
print('** nodes **')
for node in onnx_model.graph.node:
print("name=%r type=%r input=%r output=%r" % (
node.name, node.op_type, node.input, node.output))
** inputs **
[name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
, name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
, name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
]
** inputs **
name='X' dtype=1 shape=(0, 0)
name='A' dtype=1 shape=(0, 0)
name='B' dtype=1 shape=(0, 0)
** outputs **
[name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
]
** outputs **
name='Y' dtype=1 shape=(0,)
** nodes **
[input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
, input: "XA"
input: "B"
output: "Y"
op_type: "Add"
]
** nodes **
name='' type='MatMul' input=['X', 'A'] output=['XA']
name='' type='Add' input=['XA', 'B'] output=['Y']
The tensor type is an integer (= 1). The helper function onnx.helper.tensor_dtype_to_np_dtype() gives the
corresponding type with numpy.
from onnx import TensorProto
from onnx.helper import tensor_dtype_to_np_dtype, tensor_dtype_to_string
np_dtype = tensor_dtype_to_np_dtype(TensorProto.FLOAT)
print(f"The converted numpy dtype for {tensor_dtype_to_string(TensorProto.FLOAT)} is {np_dtype}.")
The converted numpy dtype for TensorProto.FLOAT is float32.
Serialization¶
ONNX is built on the top of protobuf. It adds the necessary definitions to describe a machine learning model and most of the time, ONNX is used to serialize or deserialize a model. First section addresses this need. Second section introduces the serialization and deserialization of data such as tensors, sparse tensors…
Model Serialization¶
The model needs to be saved to be deployed.
ONNX is based on protobuf. It minimizes the space needed
to save the graph on disk. Every object (see Protos)
in onnx can be serialized with method SerializeToString. That’s
the case for the whole model.
from onnx import TensorProto
from onnx.helper import (
make_model, make_node, make_graph,
make_tensor_value_info)
from onnx.checker import check_model
def shape2tuple(shape):
return tuple(getattr(d, 'dim_value', 0) for d in shape.dim)
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
graph = make_graph([node1, node2], 'lr', [X, A, B], [Y])
onnx_model = make_model(graph)
check_model(onnx_model)
# The serialization
with open("linear_regression.onnx", "wb") as f:
f.write(onnx_model.SerializeToString())
# display
print(onnx_model)
ir_version: 11
graph {
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
}
name: "lr"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
version: 23
}
The graph can be restored with function load:
from onnx import load
with open("linear_regression.onnx", "rb") as f:
onnx_model = load(f)
# display
print(onnx_model)
ir_version: 11
graph {
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
}
name: "lr"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
version: 23
}
It looks exactly the same. Any model can be serialized this way unless they are bigger than 2 Gb. protobuf is limited to size smaller than this threshold. Next sections will show how to overcome that limit.
Data Serialization¶
The serialization of tensor usually happens like the following:
import numpy
from onnx.numpy_helper import from_array
numpy_tensor = numpy.array([0, 1, 4, 5, 3], dtype=numpy.float32)
print(type(numpy_tensor))
onnx_tensor = from_array(numpy_tensor)
print(type(onnx_tensor))
serialized_tensor = onnx_tensor.SerializeToString()
print(type(serialized_tensor))
with open("saved_tensor.pb", "wb") as f:
f.write(serialized_tensor)
<class 'numpy.ndarray'>
<class 'onnx.onnx_ml_pb2.TensorProto'>
<class 'bytes'>
And the deserialization like:
from onnx import TensorProto
from onnx.numpy_helper import to_array
with open("saved_tensor.pb", "rb") as f:
serialized_tensor = f.read()
print(type(serialized_tensor))
onnx_tensor = TensorProto()
onnx_tensor.ParseFromString(serialized_tensor)
print(type(onnx_tensor))
numpy_tensor = to_array(onnx_tensor)
print(numpy_tensor)
<class 'bytes'>
<class 'onnx.onnx_ml_pb2.TensorProto'>
[0. 1. 4. 5. 3.]
The same schema can be used for but not limited to TensorProto:
import onnx
import pprint
pprint.pprint([p for p in dir(onnx)
if p.endswith('Proto') and p[0] != '_'])
['AttributeProto',
'FunctionProto',
'GraphProto',
'MapProto',
'ModelProto',
'NodeProto',
'OperatorProto',
'OperatorSetIdProto',
'OperatorSetProto',
'OptionalProto',
'SequenceProto',
'SparseTensorProto',
'StringStringEntryProto',
'TensorProto',
'TensorShapeProto',
'TrainingInfoProto',
'TypeProto',
'ValueInfoProto']
This code can be simplified with function load_tensor_from_string (see Load a Proto).
from onnx import load_tensor_from_string
with open("saved_tensor.pb", "rb") as f:
serialized = f.read()
proto = load_tensor_from_string(serialized)
print(type(proto))
<class 'onnx.onnx_ml_pb2.TensorProto'>
Initializer, default value¶
The previous model assumed the coefficients of the linear regression
were also input of the model. That’s not very convenient. They should be
part of the model itself as constant or initializer to follow
onnx semantic. Next example modifies the previous one to change inputs
A and B into initializers. The package implements two functions to
convert from numpy into onnx and the other way around
(see array).
onnx.numpy_helper.to_array: converts from onnx to numpyonnx.numpy_helper.from_array: converts from numpy to onnx
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, make_graph,
make_tensor_value_info)
from onnx.checker import check_model
# initializers
value = numpy.array([0.5, -0.6], dtype=numpy.float32)
A = numpy_helper.from_array(value, name='A')
value = numpy.array([0.4], dtype=numpy.float32)
C = numpy_helper.from_array(value, name='C')
# the part which does not change
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node1 = make_node('MatMul', ['X', 'A'], ['AX'])
node2 = make_node('Add', ['AX', 'C'], ['Y'])
graph = make_graph([node1, node2], 'lr', [X], [Y], [A, C])
onnx_model = make_model(graph)
check_model(onnx_model)
print(onnx_model)
ir_version: 11
graph {
node {
input: "X"
input: "A"
output: "AX"
op_type: "MatMul"
}
node {
input: "AX"
input: "C"
output: "Y"
op_type: "Add"
}
name: "lr"
initializer {
dims: 2
data_type: 1
name: "A"
raw_data: "\000\000\000?\232\231\031\277"
}
initializer {
dims: 1
data_type: 1
name: "C"
raw_data: "\315\314\314>"
}
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
version: 23
}
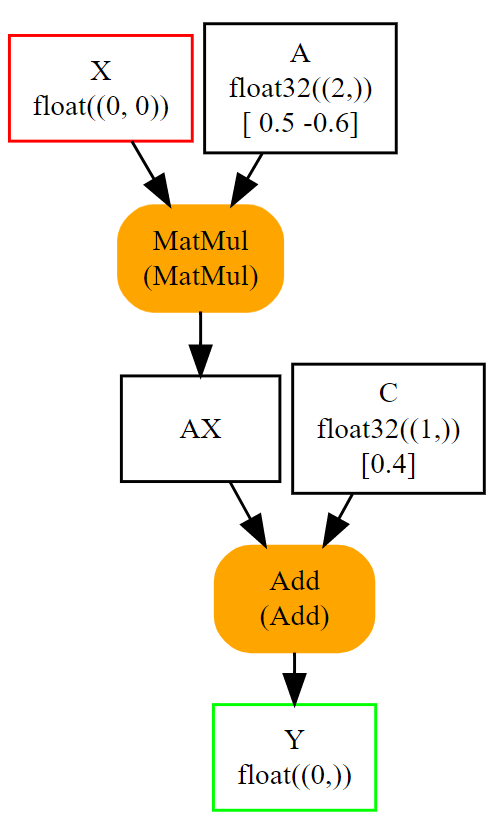
Again, it is possible to go through the onnx structure to check how the initializers look like.
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, make_graph,
make_tensor_value_info)
from onnx.checker import check_model
# initializers
value = numpy.array([0.5, -0.6], dtype=numpy.float32)
A = numpy_helper.from_array(value, name='A')
value = numpy.array([0.4], dtype=numpy.float32)
C = numpy_helper.from_array(value, name='C')
# the part which does not change
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node1 = make_node('MatMul', ['X', 'A'], ['AX'])
node2 = make_node('Add', ['AX', 'C'], ['Y'])
graph = make_graph([node1, node2], 'lr', [X], [Y], [A, C])
onnx_model = make_model(graph)
check_model(onnx_model)
print('** initializer **')
for init in onnx_model.graph.initializer:
print(init)
** initializer **
dims: 2
data_type: 1
name: "A"
raw_data: "\000\000\000?\232\231\031\277"
dims: 1
data_type: 1
name: "C"
raw_data: "\315\314\314>"
The type is defined as integer as well with the same meaning.
In this second example, there is only one input left.
Input A and B were removed. They could be kept. In that case,
they are optional: every initiliazer sharing the same name as input
is considered as a default value. It replaces the input if this one
is not given.
Attributes¶
Some operators need attributes such as Transpose operator.
Let’s build the graph for expression \(y = XA' + B\) or
y = Add(MatMul(X, Transpose(A)) + B). Transpose needs an attribute
defining the permutation of axes: perm=[1, 0]. It is added
as a named attribute in function make_node.
from onnx import TensorProto
from onnx.helper import (
make_model, make_node, make_graph,
make_tensor_value_info)
from onnx.checker import check_model
# unchanged
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
# added
node_transpose = make_node('Transpose', ['A'], ['tA'], perm=[1, 0])
# unchanged except A is replaced by tA
node1 = make_node('MatMul', ['X', 'tA'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
# node_transpose is added to the list
graph = make_graph([node_transpose, node1, node2],
'lr', [X, A, B], [Y])
onnx_model = make_model(graph)
check_model(onnx_model)
# the work is done, let's display it...
print(onnx_model)
ir_version: 11
graph {
node {
input: "A"
output: "tA"
op_type: "Transpose"
attribute {
name: "perm"
ints: 1
ints: 0
type: INTS
}
}
node {
input: "X"
input: "tA"
output: "XA"
op_type: "MatMul"
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
}
name: "lr"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
version: 23
}
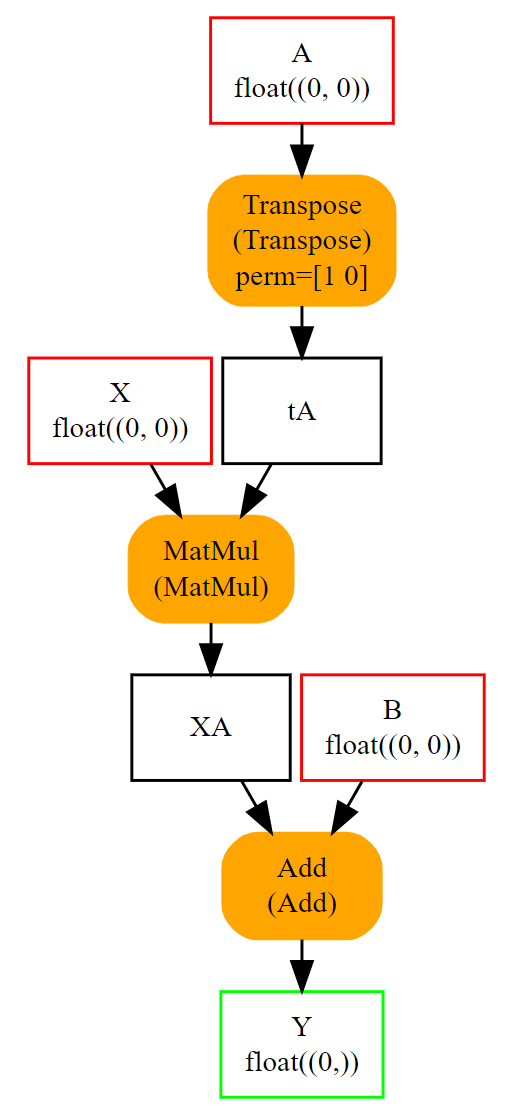
The whole list of make functions is the following. Many of them are described in section make function.
import onnx
import pprint
pprint.pprint([k for k in dir(onnx.helper)
if k.startswith('make')])
['make_attribute',
'make_attribute_ref',
'make_empty_tensor_value_info',
'make_function',
'make_graph',
'make_map',
'make_map_type_proto',
'make_model',
'make_model_gen_version',
'make_node',
'make_operatorsetid',
'make_opsetid',
'make_optional',
'make_optional_type_proto',
'make_sequence',
'make_sequence_type_proto',
'make_sparse_tensor',
'make_sparse_tensor_type_proto',
'make_sparse_tensor_value_info',
'make_tensor',
'make_tensor_sequence_value_info',
'make_tensor_type_proto',
'make_tensor_value_info',
'make_training_info',
'make_value_info']
Opset and metadata¶
Let’s load the ONNX file previously created and check what kind of metadata it has.
from onnx import load
with open("linear_regression.onnx", "rb") as f:
onnx_model = load(f)
for field in ['doc_string', 'domain', 'functions',
'ir_version', 'metadata_props', 'model_version',
'opset_import', 'producer_name', 'producer_version',
'training_info']:
print(field, getattr(onnx_model, field))
doc_string
domain
functions []
ir_version 11
metadata_props []
model_version 0
opset_import [version: 23
]
producer_name
producer_version
training_info []
Most of them are empty because it was not filled when the ONNX graph was created. Two of them have a value:
from onnx import load
with open("linear_regression.onnx", "rb") as f:
onnx_model = load(f)
print("ir_version:", onnx_model.ir_version)
for opset in onnx_model.opset_import:
print("opset domain=%r version=%r" % (opset.domain, opset.version))
ir_version: 11
opset domain='' version=23
IR defined the version of ONNX language.
Opset defines the version of operators being used.
Without any precision, ONNX uses the latest version available
coming from the installed package.
Another one can be used.
from onnx import load
with open("linear_regression.onnx", "rb") as f:
onnx_model = load(f)
del onnx_model.opset_import[:]
opset = onnx_model.opset_import.add()
opset.domain = ''
opset.version = 14
for opset in onnx_model.opset_import:
print("opset domain=%r version=%r" % (opset.domain, opset.version))
opset domain='' version=14
Any opset can be used as long as all operators are defined the way ONNX specifies it. Version 5 of operator Reshape defines the shape as an input and not as an attribute like in version 1. The opset tells which specifications is followed while describing the graph.
The other metadata can be used to store any information, to store information about the way the model was generated, a way to distinguish a model from another one with a version number.
from onnx import load, helper
with open("linear_regression.onnx", "rb") as f:
onnx_model = load(f)
onnx_model.model_version = 15
onnx_model.producer_name = "something"
onnx_model.producer_version = "some other thing"
onnx_model.doc_string = "documentation about this model"
prop = onnx_model.metadata_props
data = dict(key1="value1", key2="value2")
helper.set_model_props(onnx_model, data)
print(onnx_model)
ir_version: 11
producer_name: "something"
producer_version: "some other thing"
model_version: 15
doc_string: "documentation about this model"
graph {
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
}
name: "lr"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
version: 23
}
metadata_props {
key: "key1"
value: "value1"
}
metadata_props {
key: "key2"
value: "value2"
}
Field training_info can be used to store additional graphs.
See training_tool_test.py
to see how it works.
Subgraph: test and loops¶
They are usually grouped in a category called control flow. It is usually better to avoid them as they are not as efficient as the matrix operation are much faster and optimized.
If¶
A test can be implemented with operator If. It executes one subgraph or another depending on one boolean. This is not used very often as a function usually needs the result of many comparisons in a batch. The following example computes the sum of all floats in a matrix based on the sign, returns 1 or -1.
import numpy
import onnx
from onnx.helper import (
make_node, make_graph, make_model, make_tensor_value_info)
from onnx.numpy_helper import from_array
from onnx.checker import check_model
from onnxruntime import InferenceSession
# initializers
value = numpy.array([0], dtype=numpy.float32)
zero = from_array(value, name='zero')
# Same as before, X is the input, Y is the output.
X = make_tensor_value_info('X', onnx.TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', onnx.TensorProto.FLOAT, [None])
# The node building the condition. The first one
# sum over all axes.
rsum = make_node('ReduceSum', ['X'], ['rsum'])
# The second compares the result to 0.
cond = make_node('Greater', ['rsum', 'zero'], ['cond'])
# Builds the graph is the condition is True.
# Input for then
then_out = make_tensor_value_info(
'then_out', onnx.TensorProto.FLOAT, None)
# The constant to return.
then_cst = from_array(numpy.array([1]).astype(numpy.float32))
# The only node.
then_const_node = make_node(
'Constant', inputs=[],
outputs=['then_out'],
value=then_cst, name='cst1')
# And the graph wrapping these elements.
then_body = make_graph(
[then_const_node], 'then_body', [], [then_out])
# Same process for the else branch.
else_out = make_tensor_value_info(
'else_out', onnx.TensorProto.FLOAT, [5])
else_cst = from_array(numpy.array([-1]).astype(numpy.float32))
else_const_node = make_node(
'Constant', inputs=[],
outputs=['else_out'],
value=else_cst, name='cst2')
else_body = make_graph(
[else_const_node], 'else_body',
[], [else_out])
# Finally the node If taking both graphs as attributes.
if_node = onnx.helper.make_node(
'If', ['cond'], ['Y'],
then_branch=then_body,
else_branch=else_body)
# The final graph.
graph = make_graph([rsum, cond, if_node], 'if', [X], [Y], [zero])
onnx_model = make_model(graph)
check_model(onnx_model)
# Let's freeze the opset.
del onnx_model.opset_import[:]
opset = onnx_model.opset_import.add()
opset.domain = ''
opset.version = 15
onnx_model.ir_version = 8
# Save.
with open("onnx_if_sign.onnx", "wb") as f:
f.write(onnx_model.SerializeToString())
# Let's see the output.
sess = InferenceSession(onnx_model.SerializeToString(),
providers=["CPUExecutionProvider"])
x = numpy.ones((3, 2), dtype=numpy.float32)
res = sess.run(None, {'X': x})
# It works.
print("result", res)
print()
# Some display.
print(onnx_model)
result [array([1.], dtype=float32)]
ir_version: 8
graph {
node {
input: "X"
output: "rsum"
op_type: "ReduceSum"
}
node {
input: "rsum"
input: "zero"
output: "cond"
op_type: "Greater"
}
node {
input: "cond"
output: "Y"
op_type: "If"
attribute {
name: "else_branch"
g {
node {
output: "else_out"
name: "cst2"
op_type: "Constant"
attribute {
name: "value"
t {
dims: 1
data_type: 1
raw_data: "\000\000\200\277"
}
type: TENSOR
}
}
name: "else_body"
output {
name: "else_out"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 5
}
}
}
}
}
}
type: GRAPH
}
attribute {
name: "then_branch"
g {
node {
output: "then_out"
name: "cst1"
op_type: "Constant"
attribute {
name: "value"
t {
dims: 1
data_type: 1
raw_data: "\000\000\200?"
}
type: TENSOR
}
}
name: "then_body"
output {
name: "then_out"
type {
tensor_type {
elem_type: 1
}
}
}
}
type: GRAPH
}
}
name: "if"
initializer {
dims: 1
data_type: 1
name: "zero"
raw_data: "\000\000\000\000"
}
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
domain: ""
version: 15
}
The whole is easier to visualize with the following image.
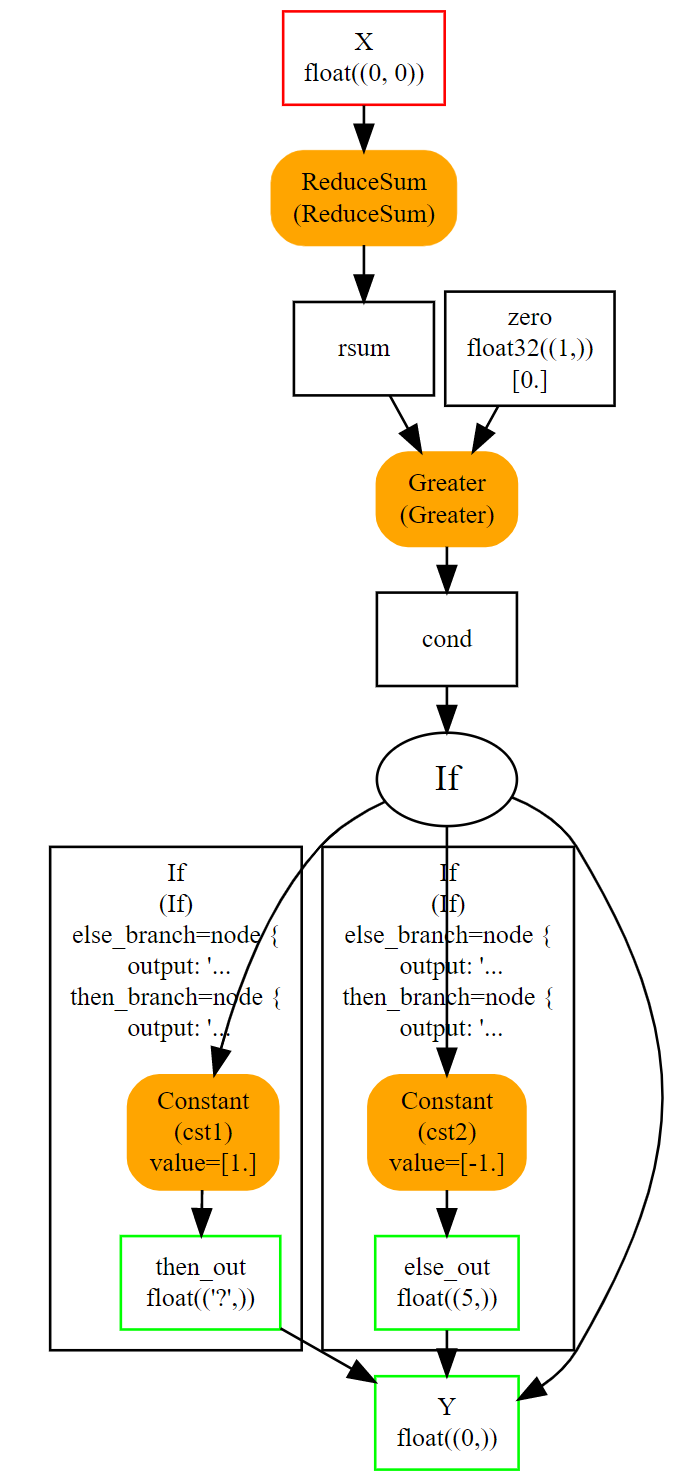
Both else and then branches are very simple. Node If could even be replaced with a node Where and that would be faster. It becomes interesting when both branches are bigger and skipping one is more efficient.
Scan¶
Scan seems quite complex when reading the specifications. It is useful to loop over one dimension of a tensor and store the results in a preallocated tensor.
The following example implements a classic nearest neighbors for a regression problem. The first step consists in computing the pairwise distances between the input features X and the training set W: \(dist(X,W) = (M_{ij}) = (\norm{X_i - W_j}^2)_{ij}\). It is followed by an operator TopK which extracts the k nearest neighbors.
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor, make_graph,
make_tensor_value_info)
from onnx.checker import check_model
# subgraph
initializers = []
nodes = []
inputs = []
outputs = []
value = make_tensor_value_info('next_in', 1, [None, 4])
inputs.append(value)
value = make_tensor_value_info('next', 1, [None])
inputs.append(value)
value = make_tensor_value_info('next_out', 1, [None, None])
outputs.append(value)
value = make_tensor_value_info('scan_out', 1, [None])
outputs.append(value)
node = make_node(
'Identity', ['next_in'], ['next_out'],
name='cdistd_17_Identity', domain='')
nodes.append(node)
node = make_node(
'Sub', ['next_in', 'next'], ['cdistdf_17_C0'],
name='cdistdf_17_Sub', domain='')
nodes.append(node)
node = make_node(
'ReduceSumSquare', ['cdistdf_17_C0'], ['cdistdf_17_reduced0'],
name='cdistdf_17_ReduceSumSquare', axes=[1], keepdims=0, domain='')
nodes.append(node)
node = make_node(
'Identity', ['cdistdf_17_reduced0'],
['scan_out'], name='cdistdf_17_Identity', domain='')
nodes.append(node)
graph = make_graph(nodes, 'OnnxIdentity',
inputs, outputs, initializers)
# main graph
initializers = []
nodes = []
inputs = []
outputs = []
opsets = {'': 15, 'ai.onnx.ml': 15}
target_opset = 15 # subgraphs
# initializers
list_value = [23.29599822460675, -120.86516699239603, -144.70495899914215, -260.08772982740413,
154.65272105889147, -122.23295157108991, 247.45232560871727, -182.83789715805776,
-132.92727431421793, 147.48710175784703, 88.27761768038069, -14.87785569894749,
111.71487894705504, 301.0518319089629, -29.64235742280055, -113.78493504731911,
-204.41218591022718, 112.26561056133608, 66.04032954135549,
-229.5428380626701, -33.549262642481615, -140.95737409864623, -87.8145187836131,
-90.61397011283958, 57.185488100413366, 56.864151796743855, 77.09054590340892,
-187.72501631246712, -42.779503579806025, -21.642642730674076, -44.58517761667535,
78.56025104939847, -23.92423223842056, 234.9166231927213, -73.73512816431007,
-10.150864499514297, -70.37105466673813, 65.5755688281476, 108.68676290979731, -78.36748960443065]
value = numpy.array(list_value, dtype=numpy.float64).reshape((2, 20))
tensor = numpy_helper.from_array(
value, name='knny_ArrayFeatureExtractorcst')
initializers.append(tensor)
list_value = [1.1394007205963135, -0.6848101019859314, -1.234825849533081, 0.4023416340351105,
0.17742614448070526, 0.46278226375579834, -0.4017809331417084, -1.630198359489441,
-0.5096521973609924, 0.7774903774261475, -0.4380742907524109, -1.2527953386306763,
-1.0485529899597168, 1.950775384902954, -1.420017957687378, -1.7062702178955078,
1.8675580024719238, -0.15135720372200012, -0.9772778749465942, 0.9500884413719177,
-2.5529897212982178, -0.7421650290489197, 0.653618574142456, 0.8644362092018127,
1.5327792167663574, 0.37816253304481506, 1.4693588018417358, 0.154947429895401,
-0.6724604368209839, -1.7262825965881348, -0.35955315828323364, -0.8131462931632996,
-0.8707971572875977, 0.056165341287851334, -0.5788496732711792, -0.3115525245666504,
1.2302906513214111, -0.302302747964859, 1.202379822731018, -0.38732680678367615,
2.269754648208618, -0.18718385696411133, -1.4543657302856445, 0.04575851559638977,
-0.9072983860969543, 0.12898291647434235, 0.05194539576768875, 0.7290905714035034,
1.4940791130065918, -0.8540957570075989, -0.2051582634449005, 0.3130677044391632,
1.764052391052246, 2.2408931255340576, 0.40015721321105957, 0.978738009929657,
0.06651721894741058, -0.3627411723136902, 0.30247190594673157, -0.6343221068382263,
-0.5108051300048828, 0.4283318817615509, -1.18063223361969, -0.02818222902715206,
-1.6138978004455566, 0.38690251111984253, -0.21274028718471527, -0.8954665660858154,
0.7610377073287964, 0.3336743414402008, 0.12167501449584961, 0.44386324286460876,
-0.10321885347366333, 1.4542734622955322, 0.4105985164642334, 0.14404356479644775,
-0.8877857327461243, 0.15634897351264954, -1.980796456336975, -0.34791216254234314]
value = numpy.array(list_value, dtype=numpy.float32).reshape((20, 4))
tensor = numpy_helper.from_array(value, name='Sc_Scancst')
initializers.append(tensor)
value = numpy.array([2], dtype=numpy.int64)
tensor = numpy_helper.from_array(value, name='To_TopKcst')
initializers.append(tensor)
value = numpy.array([2, -1, 2], dtype=numpy.int64)
tensor = numpy_helper.from_array(value, name='knny_Reshapecst')
initializers.append(tensor)
# inputs
value = make_tensor_value_info('input', 1, [None, 4])
inputs.append(value)
# outputs
value = make_tensor_value_info('variable', 1, [None, 2])
outputs.append(value)
# nodes
node = make_node(
'Scan', ['input', 'Sc_Scancst'], ['UU032UU', 'UU033UU'],
name='Sc_Scan', body=graph, num_scan_inputs=1, domain='')
nodes.append(node)
node = make_node(
'Transpose', ['UU033UU'], ['Tr_transposed0'],
name='Tr_Transpose', perm=[1, 0], domain='')
nodes.append(node)
node = make_node(
'Sqrt', ['Tr_transposed0'], ['Sq_Y0'],
name='Sq_Sqrt', domain='')
nodes.append(node)
node = make_node(
'TopK', ['Sq_Y0', 'To_TopKcst'], ['To_Values0', 'To_Indices1'],
name='To_TopK', largest=0, sorted=1, domain='')
nodes.append(node)
node = make_node(
'Flatten', ['To_Indices1'], ['knny_output0'],
name='knny_Flatten', domain='')
nodes.append(node)
node = make_node(
'ArrayFeatureExtractor',
['knny_ArrayFeatureExtractorcst', 'knny_output0'], ['knny_Z0'],
name='knny_ArrayFeatureExtractor', domain='ai.onnx.ml')
nodes.append(node)
node = make_node(
'Reshape', ['knny_Z0', 'knny_Reshapecst'], ['knny_reshaped0'],
name='knny_Reshape', allowzero=0, domain='')
nodes.append(node)
node = make_node(
'Transpose', ['knny_reshaped0'], ['knny_transposed0'],
name='knny_Transpose', perm=[1, 0, 2], domain='')
nodes.append(node)
node = make_node(
'Cast', ['knny_transposed0'], ['Ca_output0'],
name='Ca_Cast', to=TensorProto.FLOAT, domain='')
nodes.append(node)
node = make_node(
'ReduceMean', ['Ca_output0'], ['variable'],
name='Re_ReduceMean', axes=[2], keepdims=0, domain='')
nodes.append(node)
# graph
graph = make_graph(nodes, 'KNN regressor', inputs, outputs, initializers)
# model
onnx_model = make_model(graph)
onnx_model.ir_version = 8
onnx_model.producer_name = 'skl2onnx'
onnx_model.producer_version = ''
onnx_model.domain = 'ai.onnx'
onnx_model.model_version = 0
onnx_model.doc_string = ''
set_model_props(onnx_model, {})
# opsets
del onnx_model.opset_import[:]
for dom, value in opsets.items():
op_set = onnx_model.opset_import.add()
op_set.domain = dom
op_set.version = value
check_model(onnx_model)
with open("knnr.onnx", "wb") as f:
f.write(onnx_model.SerializeToString())
print(onnx_model)
ir_version: 8
producer_name: "skl2onnx"
producer_version: ""
domain: "ai.onnx"
model_version: 0
doc_string: ""
graph {
node {
input: "input"
input: "Sc_Scancst"
output: "UU032UU"
output: "UU033UU"
name: "Sc_Scan"
op_type: "Scan"
attribute {
name: "body"
g {
node {
input: "next_in"
output: "next_out"
name: "cdistd_17_Identity"
op_type: "Identity"
domain: ""
}
node {
input: "next_in"
input: "next"
output: "cdistdf_17_C0"
name: "cdistdf_17_Sub"
op_type: "Sub"
domain: ""
}
node {
input: "cdistdf_17_C0"
output: "cdistdf_17_reduced0"
name: "cdistdf_17_ReduceSumSquare"
op_type: "ReduceSumSquare"
attribute {
name: "axes"
ints: 1
type: INTS
}
attribute {
name: "keepdims"
i: 0
type: INT
}
domain: ""
}
node {
input: "cdistdf_17_reduced0"
output: "scan_out"
name: "cdistdf_17_Identity"
op_type: "Identity"
domain: ""
}
name: "OnnxIdentity"
input {
name: "next_in"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
dim_value: 4
}
}
}
}
}
input {
name: "next"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
output {
name: "next_out"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "scan_out"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
type: GRAPH
}
attribute {
name: "num_scan_inputs"
i: 1
type: INT
}
domain: ""
}
node {
input: "UU033UU"
output: "Tr_transposed0"
name: "Tr_Transpose"
op_type: "Transpose"
attribute {
name: "perm"
ints: 1
ints: 0
type: INTS
}
domain: ""
}
node {
input: "Tr_transposed0"
output: "Sq_Y0"
name: "Sq_Sqrt"
op_type: "Sqrt"
domain: ""
}
node {
input: "Sq_Y0"
input: "To_TopKcst"
output: "To_Values0"
output: "To_Indices1"
name: "To_TopK"
op_type: "TopK"
attribute {
name: "largest"
i: 0
type: INT
}
attribute {
name: "sorted"
i: 1
type: INT
}
domain: ""
}
node {
input: "To_Indices1"
output: "knny_output0"
name: "knny_Flatten"
op_type: "Flatten"
domain: ""
}
node {
input: "knny_ArrayFeatureExtractorcst"
input: "knny_output0"
output: "knny_Z0"
name: "knny_ArrayFeatureExtractor"
op_type: "ArrayFeatureExtractor"
domain: "ai.onnx.ml"
}
node {
input: "knny_Z0"
input: "knny_Reshapecst"
output: "knny_reshaped0"
name: "knny_Reshape"
op_type: "Reshape"
attribute {
name: "allowzero"
i: 0
type: INT
}
domain: ""
}
node {
input: "knny_reshaped0"
output: "knny_transposed0"
name: "knny_Transpose"
op_type: "Transpose"
attribute {
name: "perm"
ints: 1
ints: 0
ints: 2
type: INTS
}
domain: ""
}
node {
input: "knny_transposed0"
output: "Ca_output0"
name: "Ca_Cast"
op_type: "Cast"
attribute {
name: "to"
i: 1
type: INT
}
domain: ""
}
node {
input: "Ca_output0"
output: "variable"
name: "Re_ReduceMean"
op_type: "ReduceMean"
attribute {
name: "axes"
ints: 2
type: INTS
}
attribute {
name: "keepdims"
i: 0
type: INT
}
domain: ""
}
name: "KNN regressor"
initializer {
dims: 2
dims: 20
data_type: 11
name: "knny_ArrayFeatureExtractorcst"
raw_data: ",\&\212\306K7@\333z`\345^7^\300\304\312,\006\217\026b\300Z9dWgAp\300.+F\027\343Tc@\203\330\264\255\350\216^\300\260\022\216sy\356n@\237h\263\r\320\332f\300\224\277.;\254\235`\300\336\370lV\226ob@\261\201\362|\304\021V@c,[Mv\301-\300\322\214\240\223\300\355[@)\036\262M\324\320r@nE;\211q\244=\300\021n5`<r\\300\207\211\201\2400\215i\300H\232p\303\377\020\@\317K[\302\224\202P@&\306\355\355^\261l\300\301/\377<N\306@\300#w\001\317\242\236a\300$fd\023!\364U\300\204\327LIK\247V\300J\211\366\022\276\227L@\262\345\254\206\234nL@f{\013\201\313ES@\234\343hU3wg\300\3370\367\305\306cE\300\336A\347;\204\2445\300f\374\242\031\347JF\300\325\2557'\333\243S@\331\354\345{\232\3547\300\307o)\372T]m@#\005\000W\014oR\300'\025\227\034>M$\300\310\252\022\\277\227Q\300l_\243\036\326dP@\333kk\354\363+[@\223)\036\363\204\227S\300"
}
initializer {
dims: 20
dims: 4
data_type: 1
name: "Sc_Scancst"
raw_data: "\342\327\221?\267O/\277\306\016\236\277\271\377\315>3\2575>\314\361\354>;\266\315\276W\252\320\277\221x\002\277\234\tG?FK\340\276\231[\240\277\3746\206\277\002\263\371?&\303\265\277\020g\332\277$\014\357?b\375\032\276\342.z\277\3778s?/d#\300\207\376=\277\214S'?\261K]?\0342\304?\205\236\301>\363\023\274?\212\252\036>^&,\277\324\366\334\277Z\027\270\276[*P\277\220\354^\277\241\rf=~/\024\277\320\203\237\276*z\235?m\307\232\276\225\347\231?\263O\306\276\251C\021@ \255?\276\250(\272\277Hm;=\265Dh\277\031\024\004>\262\304T=\256\245:?\374=\277?\005\246Z\277\002\025R\276iJ\240>x\314\341?\313j\017@h\341\314>\223\216z?.:\210=6\271\271\276\231\335\232>\357b"\277 \304\002\277QN\333>\365\036\227\277k\336\346\2744\224\316\277\026\030\306>\227\330Y\276L=e\277^\323B?]\327\252>\3000\371=\013B\343>hd\323\275\242%\272?\3709\322>(\200\023>\355Ec\277\362\031 >\275\212\375\277\213!\262\276"
}
initializer {
dims: 1
data_type: 7
name: "To_TopKcst"
raw_data: "\002\000\000\000\000\000\000\000"
}
initializer {
dims: 3
data_type: 7
name: "knny_Reshapecst"
raw_data: "\002\000\000\000\000\000\000\000\377\377\377\377\377\377\377\377\002\000\000\000\000\000\000\000"
}
input {
name: "input"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
dim_value: 4
}
}
}
}
}
output {
name: "variable"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
dim_value: 2
}
}
}
}
}
}
opset_import {
domain: ""
version: 15
}
opset_import {
domain: "ai.onnx.ml"
version: 15
}
Visually it looks like the following:
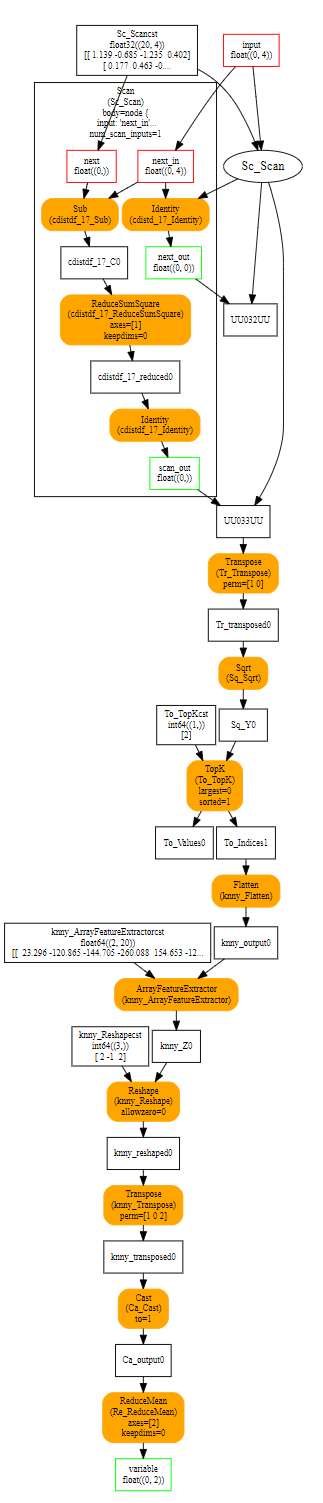
The subgraph is executed by operator Scan. In this case, there is one scan input meaning the operator only builds one output.
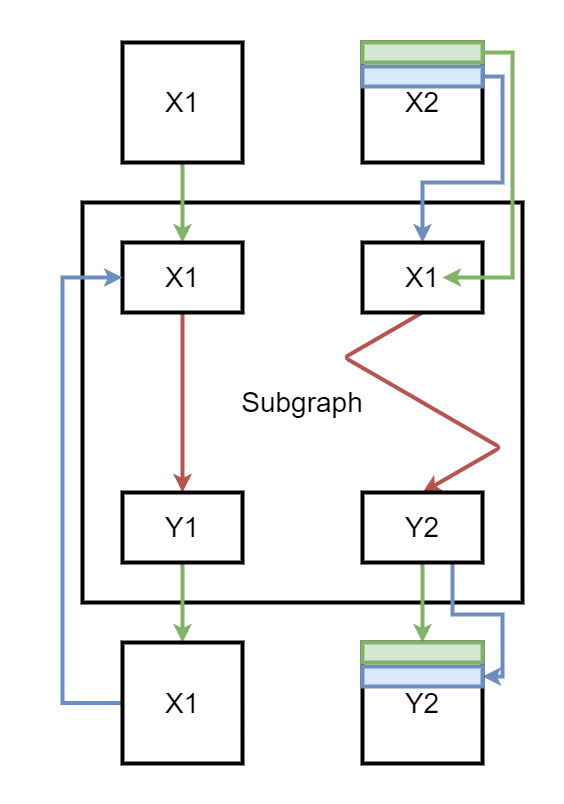
node = make_node(
'Scan', ['X1', 'X2'], ['Y1', 'Y2'],
name='Sc_Scan', body=graph, num_scan_inputs=1, domain='')
At the first iteration, the subgraph gets X1 and the first row of X2. The graph produces two outputs. The first one replaces X1 in the next iteration, the second one is store in a container to form Y2. At the second iteration, second input of the subgraph is the second row of X2. Here is a short summary. Green is the first iteration, blue the second.
Functions¶
As mentioned in previous chapter, functions can be used to shorten the code to build the model and offer more possibilities to the runtime running predictions to be faster if there exists a specific implementation of this function. If it is not the case, the runtime can still use the default implementation based on existing operators.
Function make_function is used to define a function.
It works like a graph with less types. It is more like a
template. This API may evolve. It does not include initializers either.
A function with no attribute¶
That’s the more simple case. Every input of the function is a dynamic object known at execution time.
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor,
make_graph, make_tensor_value_info, make_opsetid,
make_function)
from onnx.checker import check_model
new_domain = 'custom'
opset_imports = [make_opsetid("", 14), make_opsetid(new_domain, 1)]
# Let's define a function for a linear regression
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
linear_regression = make_function(
new_domain, # domain name
'LinearRegression', # function name
['X', 'A', 'B'], # input names
['Y'], # output names
[node1, node2], # nodes
opset_imports, # opsets
[]) # attribute names
# Let's use it in a graph.
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
graph = make_graph(
[make_node('LinearRegression', ['X', 'A', 'B'], ['Y1'], domain=new_domain),
make_node('Abs', ['Y1'], ['Y'])],
'example',
[X, A, B], [Y])
onnx_model = make_model(
graph, opset_imports=opset_imports,
functions=[linear_regression]) # functions to add)
check_model(onnx_model)
# the work is done, let's display it...
print(onnx_model)
ir_version: 11
graph {
node {
input: "X"
input: "A"
input: "B"
output: "Y1"
op_type: "LinearRegression"
domain: "custom"
}
node {
input: "Y1"
output: "Y"
op_type: "Abs"
}
name: "example"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
domain: ""
version: 14
}
opset_import {
domain: "custom"
version: 1
}
functions {
name: "LinearRegression"
input: "X"
input: "A"
input: "B"
output: "Y"
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
}
opset_import {
domain: ""
version: 14
}
opset_import {
domain: "custom"
version: 1
}
domain: "custom"
}
A function with attributes¶
The following functions are equivalent to the previous one except
one input, B, was converted into an argument named bias.
The code is almost the same except the bias is now a constant.
Inside the function definition, a node Constant is created
to insert the argument as a result. It is linked to the argument
with the attribute ref_attr_name.
import numpy
from onnx import numpy_helper, TensorProto, AttributeProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor,
make_graph, make_tensor_value_info, make_opsetid,
make_function)
from onnx.checker import check_model
new_domain = 'custom'
opset_imports = [make_opsetid("", 14), make_opsetid(new_domain, 1)]
# Let's define a function for a linear regression
# The first step consists in creating a constant
# equal to the input parameter of the function.
cst = make_node('Constant', [], ['B'])
att = AttributeProto()
att.name = "value"
# This line indicates the value comes from the argument
# named 'bias' the function is given.
att.ref_attr_name = "bias"
att.type = AttributeProto.TENSOR
cst.attribute.append(att)
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
linear_regression = make_function(
new_domain, # domain name
'LinearRegression', # function name
['X', 'A'], # input names
['Y'], # output names
[cst, node1, node2], # nodes
opset_imports, # opsets
["bias"]) # attribute names
# Let's use it in a graph.
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
graph = make_graph(
[make_node('LinearRegression', ['X', 'A'], ['Y1'], domain=new_domain,
# bias is now an argument of the function and is defined as a tensor
bias=make_tensor('former_B', TensorProto.FLOAT, [1], [0.67])),
make_node('Abs', ['Y1'], ['Y'])],
'example',
[X, A], [Y])
onnx_model = make_model(
graph, opset_imports=opset_imports,
functions=[linear_regression]) # functions to add)
check_model(onnx_model)
# the work is done, let's display it...
print(onnx_model)
ir_version: 11
graph {
node {
input: "X"
input: "A"
output: "Y1"
op_type: "LinearRegression"
attribute {
name: "bias"
t {
dims: 1
data_type: 1
float_data: 0.67
name: "former_B"
}
type: TENSOR
}
domain: "custom"
}
node {
input: "Y1"
output: "Y"
op_type: "Abs"
}
name: "example"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
dim {
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
}
}
}
}
}
}
opset_import {
domain: ""
version: 14
}
opset_import {
domain: "custom"
version: 1
}
functions {
name: "LinearRegression"
input: "X"
input: "A"
output: "Y"
attribute: "bias"
node {
output: "B"
op_type: "Constant"
attribute {
name: "value"
type: TENSOR
ref_attr_name: "bias"
}
}
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
}
opset_import {
domain: ""
version: 14
}
opset_import {
domain: "custom"
version: 1
}
domain: "custom"
}
Parsing¶
Module onnx provides a faster way to define a graph and is lot easier to read. That’s easy to use when the graph is built in a single function, less easy when the graph is built from many different functions converting each piece of a machine learning pipeline.
import onnx.parser
from onnx.checker import check_model
input = '''
<
ir_version: 8,
opset_import: [ "" : 15]
>
agraph (float[I,J] X, float[I] A, float[I] B) => (float[I] Y) {
XA = MatMul(X, A)
Y = Add(XA, B)
}
'''
onnx_model = onnx.parser.parse_model(input)
check_model(onnx_model)
print(onnx_model)
ir_version: 8
graph {
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
domain: ""
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
domain: ""
}
name: "agraph"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_param: "I"
}
dim {
dim_param: "J"
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_param: "I"
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_param: "I"
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_param: "I"
}
}
}
}
}
}
opset_import {
domain: ""
version: 15
}
This way is used to create small models but it is rarely used in converting libraries.
Checker and Shape Inference¶
onnx provides a function to check the model is valid. It checks input type or shapes whenever it can detect inconsistency. The following example adds two matrices of different types which is not allowed.
import onnx.parser
import onnx.checker
input = '''
<
ir_version: 8,
opset_import: [ "" : 15]
>
agraph (float[I,4] X, float[4,2] A, int[4] B) => (float[I] Y) {
XA = MatMul(X, A)
Y = Add(XA, B)
}
'''
try:
onnx_model = onnx.parser.parse_model(input)
onnx.checker.check_model(onnx_model)
except Exception as e:
print(e)
b'[ParseError at position (line: 6 column: 44)]\nError context: agraph (float[I,4] X, float[4,2] A, int[4] B) => (float[I] Y) {\nExpected character ) not found.'
check_model raises an error due to that inconsistency.
This work for all operators defined in the main domain or the ML domain.
It remains silent for any custom operator not defined in any specification.
Shape inference serves one purpose: estimate the shape and the type of intermediate results. If known, the runtime can estimate the memory consumption beforehand and optimize the computation. It can fuse some operators, it can do the computation inplace…
import onnx.parser
from onnx import helper, shape_inference
input = '''
<
ir_version: 8,
opset_import: [ "" : 15]
>
agraph (float[I,4] X, float[4,2] A, float[4] B) => (float[I] Y) {
XA = MatMul(X, A)
Y = Add(XA, B)
}
'''
onnx_model = onnx.parser.parse_model(input)
inferred_model = shape_inference.infer_shapes(onnx_model)
print(inferred_model)
ir_version: 8
graph {
node {
input: "X"
input: "A"
output: "XA"
op_type: "MatMul"
domain: ""
}
node {
input: "XA"
input: "B"
output: "Y"
op_type: "Add"
domain: ""
}
name: "agraph"
input {
name: "X"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_param: "I"
}
dim {
dim_value: 4
}
}
}
}
}
input {
name: "A"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 4
}
dim {
dim_value: 2
}
}
}
}
}
input {
name: "B"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_value: 4
}
}
}
}
}
output {
name: "Y"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_param: "I"
}
}
}
}
}
value_info {
name: "XA"
type {
tensor_type {
elem_type: 1
shape {
dim {
dim_param: "I"
}
dim {
dim_value: 2
}
}
}
}
}
}
opset_import {
domain: ""
version: 15
}
There is a new attribute value_info which stores the inferred shapes.
Letter I in dim_param: "I" can be seen as a variable. It depends on the inputs
but the function is able to tell which intermediate result will share
the same dimension.
Shape inference does not work all the time. For example,
a Reshape operator. Shape inference only works if the shape is constant.
If not constant, the shape cannot be easily inferred unless
the following nodes expect specific shape.
Evaluation and Runtime¶
The ONNX standard allows frameworks to export trained models in ONNX format, and enables inference using any backend that supports the ONNX format. onnxruntime is one efficient option. It is available in many platforms. It is optimized for fast inference. Its coverage can be tracked on ONNX Backend Dashboard. onnx implements a python runtime useful to help understand a model. It is not intended to be used for production and performance is not a goal.
Evaluation of a linear regression¶
Full API is described at onnx.reference.
It takes a model (a ModelProto, a filename, …).
Method run returns the outputs for a given set of inputs
specified in a dictionary.
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor,
make_graph, make_tensor_value_info)
from onnx.checker import check_model
from onnx.reference import ReferenceEvaluator
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
graph = make_graph([node1, node2], 'lr', [X, A, B], [Y])
onnx_model = make_model(graph)
check_model(onnx_model)
sess = ReferenceEvaluator(onnx_model)
x = numpy.random.randn(4, 2).astype(numpy.float32)
a = numpy.random.randn(2, 1).astype(numpy.float32)
b = numpy.random.randn(1, 1).astype(numpy.float32)
feeds = {'X': x, 'A': a, 'B': b}
print(sess.run(None, feeds))
[array([[ 1.0621979 ],
[-0.31870604],
[ 1.3411267 ],
[-0.24864137]], dtype=float32)]
Evaluation of a node¶
The evaluator can also evaluate a simple node to check how an operator behaves on a specific input.
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import make_node
from onnx.reference import ReferenceEvaluator
node = make_node('EyeLike', ['X'], ['Y'])
sess = ReferenceEvaluator(node)
x = numpy.random.randn(4, 2).astype(numpy.float32)
feeds = {'X': x}
print(sess.run(None, feeds))
[array([[1., 0.],
[0., 1.],
[0., 0.],
[0., 0.]], dtype=float32)]
Similar code would also work on GraphProto or FunctionProto.
Evaluation Step by Step¶
A converting library takes an existing model trained with a machine
learning framework (pytorch, scikit-learn, …) and
converts the model into an ONNX graph. Complex models usually do not work
on the first try and seeing intermediate results may help to find the
part incorrectly converted. Parameter verbose displays information
about intermediate results.
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor,
make_graph, make_tensor_value_info)
from onnx.checker import check_model
from onnx.reference import ReferenceEvaluator
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'B'], ['Y'])
graph = make_graph([node1, node2], 'lr', [X, A, B], [Y])
onnx_model = make_model(graph)
check_model(onnx_model)
for verbose in [1, 2, 3, 4]:
print()
print(f"------ verbose={verbose}")
print()
sess = ReferenceEvaluator(onnx_model, verbose=verbose)
x = numpy.random.randn(4, 2).astype(numpy.float32)
a = numpy.random.randn(2, 1).astype(numpy.float32)
b = numpy.random.randn(1, 1).astype(numpy.float32)
feeds = {'X': x, 'A': a, 'B': b}
print(sess.run(None, feeds))
------ verbose=1
[array([[-3.5899534],
[-1.5545228],
[-3.0967803],
[-3.6525843]], dtype=float32)]
------ verbose=2
MatMul(X, A) -> XA
Add(XA, B) -> Y
[array([[4.116333 ],
[4.9032254],
[3.030632 ],
[3.6492145]], dtype=float32)]
------ verbose=3
+I X: float32:(4, 2) in [-1.283676028251648, 0.9766603708267212]
+I A: float32:(2, 1) in [0.1504102349281311, 1.5227805376052856]
+I B: float32:(1, 1) in [-0.2273963838815689, -0.2273963838815689]
MatMul(X, A) -> XA
+ XA: float32:(4, 1) in [-1.3283635377883911, 0.3365260660648346]
Add(XA, B) -> Y
+ Y: float32:(4, 1) in [-1.5557599067687988, 0.10912968218326569]
[array([[-1.4018838 ],
[-0.314448 ],
[ 0.10912968],
[-1.5557599 ]], dtype=float32)]
------ verbose=4
+I X: float32:(4, 2):1.1508103609085083,1.5402522087097168,-0.22718697786331177,0.905017077922821,-0.6978850364685059...
+I A: float32:(2, 1):[-1.0623019933700562, -0.5758040547370911]
+I B: float32:(1, 1):[0.24835994839668274]
MatMul(X, A) -> XA
+ XA: float32:(4, 1):[-2.109391689300537, -0.2797713279724121, 0.42591774463653564, 0.38503438234329224]
Add(XA, B) -> Y
+ Y: float32:(4, 1):[-1.8610317707061768, -0.03141137957572937, 0.674277663230896, 0.6333943605422974]
[array([[-1.8610318 ],
[-0.03141138],
[ 0.67427766],
[ 0.63339436]], dtype=float32)]
Evaluate a custom node¶
The following example still implements a linear regression but adds the identity matrix to A: \(Y = X(A + I) + B\).
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor,
make_graph, make_tensor_value_info)
from onnx.checker import check_model
from onnx.reference import ReferenceEvaluator
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node0 = make_node('EyeLike', ['A'], ['Eye'])
node1 = make_node('Add', ['A', 'Eye'], ['A1'])
node2 = make_node('MatMul', ['X', 'A1'], ['XA1'])
node3 = make_node('Add', ['XA1', 'B'], ['Y'])
graph = make_graph([node0, node1, node2, node3], 'lr', [X, A, B], [Y])
onnx_model = make_model(graph)
check_model(onnx_model)
with open("linear_regression.onnx", "wb") as f:
f.write(onnx_model.SerializeToString())
sess = ReferenceEvaluator(onnx_model, verbose=2)
x = numpy.random.randn(4, 2).astype(numpy.float32)
a = numpy.random.randn(2, 2).astype(numpy.float32) / 10
b = numpy.random.randn(1, 2).astype(numpy.float32)
feeds = {'X': x, 'A': a, 'B': b}
print(sess.run(None, feeds))
EyeLike(A) -> Eye
Add(A, Eye) -> A1
MatMul(X, A1) -> XA1
Add(XA1, B) -> Y
[array([[-1.3991715 , -0.24793124],
[-1.8714755 , -3.2171514 ],
[-0.78722763, 0.571173 ],
[-1.9286282 , -1.8162231 ]], dtype=float32)]
What if we combine operators EyeLike and Add into AddEyeLike to
make it more efficient. Next example replaces these two operators
by a single one from domain 'optimized'.
import numpy
from onnx import numpy_helper, TensorProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor,
make_graph, make_tensor_value_info, make_opsetid)
from onnx.checker import check_model
X = make_tensor_value_info('X', TensorProto.FLOAT, [None, None])
A = make_tensor_value_info('A', TensorProto.FLOAT, [None, None])
B = make_tensor_value_info('B', TensorProto.FLOAT, [None, None])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, [None])
node01 = make_node('AddEyeLike', ['A'], ['A1'], domain='optimized')
node2 = make_node('MatMul', ['X', 'A1'], ['XA1'])
node3 = make_node('Add', ['XA1', 'B'], ['Y'])
graph = make_graph([node01, node2, node3], 'lr', [X, A, B], [Y])
onnx_model = make_model(graph, opset_imports=[
make_opsetid('', 18), make_opsetid('optimized', 1)
])
check_model(onnx_model)
with open("linear_regression_improved.onnx", "wb") as f:
f.write(onnx_model.SerializeToString())
We need to evaluate this model is equivalent to the first one. This requires an implementation for this particular node.
import numpy
from onnx.reference import ReferenceEvaluator
from onnx.reference.op_run import OpRun
class AddEyeLike(OpRun):
op_domain = "optimized"
def _run(self, X, alpha=1.):
assert len(X.shape) == 2
assert X.shape[0] == X.shape[1]
X = X.copy()
ind = numpy.diag_indices(X.shape[0])
X[ind] += alpha
return (X,)
sess = ReferenceEvaluator("linear_regression_improved.onnx", verbose=2, new_ops=[AddEyeLike])
x = numpy.random.randn(4, 2).astype(numpy.float32)
a = numpy.random.randn(2, 2).astype(numpy.float32) / 10
b = numpy.random.randn(1, 2).astype(numpy.float32)
feeds = {'X': x, 'A': a, 'B': b}
print(sess.run(None, feeds))
# Let's check with the previous model.
sess0 = ReferenceEvaluator("linear_regression.onnx",)
sess1 = ReferenceEvaluator("linear_regression_improved.onnx", new_ops=[AddEyeLike])
y0 = sess0.run(None, feeds)[0]
y1 = sess1.run(None, feeds)[0]
print(y0)
print(y1)
print(f"difference: {numpy.abs(y0 - y1).max()}")
AddEyeLike(A) -> A1
MatMul(X, A1) -> XA1
Add(XA1, B) -> Y
[array([[-1.1433096 , -1.1836832 ],
[-0.78761196, -1.6567395 ],
[-3.7504854 , -3.3158715 ],
[-1.8096153 , -1.8507305 ]], dtype=float32)]
[[-1.1433096 -1.1836832 ]
[-0.78761196 -1.6567395 ]
[-3.7504854 -3.3158715 ]
[-1.8096153 -1.8507305 ]]
[[-1.1433096 -1.1836832 ]
[-0.78761196 -1.6567395 ]
[-3.7504854 -3.3158715 ]
[-1.8096153 -1.8507305 ]]
difference: 0.0
Predictions are the same. Let’s compare the performance on a matrix big enough to see a significant difference.
import timeit
import numpy
from onnx.reference import ReferenceEvaluator
from onnx.reference.op_run import OpRun
class AddEyeLike(OpRun):
op_domain = "optimized"
def _run(self, X, alpha=1.):
assert len(X.shape) == 2
assert X.shape[0] == X.shape[1]
X = X.copy()
ind = numpy.diag_indices(X.shape[0])
X[ind] += alpha
return (X,)
sess = ReferenceEvaluator("linear_regression_improved.onnx", verbose=2, new_ops=[AddEyeLike])
x = numpy.random.randn(4, 100).astype(numpy.float32)
a = numpy.random.randn(100, 100).astype(numpy.float32) / 10
b = numpy.random.randn(1, 100).astype(numpy.float32)
feeds = {'X': x, 'A': a, 'B': b}
sess0 = ReferenceEvaluator("linear_regression.onnx")
sess1 = ReferenceEvaluator("linear_regression_improved.onnx", new_ops=[AddEyeLike])
y0 = sess0.run(None, feeds)[0]
y1 = sess1.run(None, feeds)[0]
print(f"difference: {numpy.abs(y0 - y1).max()}")
print(f"time with EyeLike+Add: {timeit.timeit(lambda: sess0.run(None, feeds), number=1000)}")
print(f"time with AddEyeLike: {timeit.timeit(lambda: sess1.run(None, feeds), number=1000)}")
difference: 0.0
time with EyeLike+Add: 0.09169735500006482
time with AddEyeLike: 0.0725484490000099
It seems worth adding an optimized node in this case. This kind of optimization is usually called fusion. Two consecutive operators are fused into an optimized version of both. Production usually relies on onnxruntime but since the optimization uses basic matrix operation, it should bring the same performance gain on any other runtime.
Implementation details¶
Python and C++¶
onnx relies on protobuf to define its type.
You would assume that a python object is just a wrapper around
a C pointer on the internal structure. Therefore, it should be
possible to access internal data from a function receiving a python
object of type ModelProto. But it is not. According to
Protobuf 4, changes,
this is no longer possible after version 4 and it is safer to assume the
only way to get a hold on the content is to serialize the model
into bytes, give it to the C function, then deserialize it.
Functions like check_model or
shape_inference are calling SerializeToString then
ParseFromString before checking the model with a C code.
Attributes and inputs¶
There is a clear distinction between the two. Inputs are dynamic and may change at every execution. Attributes never changes and an optimizer can improve the execution graph assuming it never changes. Therefore, it is impossible to turn an input into an attribute. And the operator Constant is the only operator changing an attribute into an input.
Shape or no shape¶
onnx usually expects a shape for every input or output assuming the rank (or the number of dimensions) is known. What if we need to create a valid graph for every dimension? This case is still puzzling.
import numpy
from onnx import numpy_helper, TensorProto, FunctionProto
from onnx.helper import (
make_model, make_node, set_model_props, make_tensor,
make_graph, make_tensor_value_info, make_opsetid,
make_function)
from onnx.checker import check_model
from onnxruntime import InferenceSession
def create_model(shapes):
new_domain = 'custom'
opset_imports = [make_opsetid("", 14), make_opsetid(new_domain, 1)]
node1 = make_node('MatMul', ['X', 'A'], ['XA'])
node2 = make_node('Add', ['XA', 'A'], ['Y'])
X = make_tensor_value_info('X', TensorProto.FLOAT, shapes['X'])
A = make_tensor_value_info('A', TensorProto.FLOAT, shapes['A'])
Y = make_tensor_value_info('Y', TensorProto.FLOAT, shapes['Y'])
graph = make_graph([node1, node2], 'example', [X, A], [Y])
onnx_model = make_model(graph, opset_imports=opset_imports)
# Let models runnable by onnxruntime with a released ir_version
onnx_model.ir_version = 8
return onnx_model
print("----------- case 1: 2D x 2D -> 2D")
onnx_model = create_model({'X': [None, None], 'A': [None, None], 'Y': [None, None]})
check_model(onnx_model)
sess = InferenceSession(onnx_model.SerializeToString(),
providers=["CPUExecutionProvider"])
res = sess.run(None, {
'X': numpy.random.randn(2, 2).astype(numpy.float32),
'A': numpy.random.randn(2, 2).astype(numpy.float32)})
print(res)
print("----------- case 2: 2D x 1D -> 1D")
onnx_model = create_model({'X': [None, None], 'A': [None], 'Y': [None]})
check_model(onnx_model)
sess = InferenceSession(onnx_model.SerializeToString(),
providers=["CPUExecutionProvider"])
res = sess.run(None, {
'X': numpy.random.randn(2, 2).astype(numpy.float32),
'A': numpy.random.randn(2).astype(numpy.float32)})
print(res)
print("----------- case 3: 2D x 0D -> 0D")
onnx_model = create_model({'X': [None, None], 'A': [], 'Y': []})
check_model(onnx_model)
try:
InferenceSession(onnx_model.SerializeToString(),
providers=["CPUExecutionProvider"])
except Exception as e:
print(e)
print("----------- case 4: 2D x None -> None")
onnx_model = create_model({'X': [None, None], 'A': None, 'Y': None})
try:
check_model(onnx_model)
except Exception as e:
print(type(e), e)
sess = InferenceSession(onnx_model.SerializeToString(),
providers=["CPUExecutionProvider"])
res = sess.run(None, {
'X': numpy.random.randn(2, 2).astype(numpy.float32),
'A': numpy.random.randn(2).astype(numpy.float32)})
print(res)
print("----------- end")
----------- case 1: 2D x 2D -> 2D
[array([[ 1.9142151, -2.887577 ],
[-1.8545747, -1.2522402]], dtype=float32)]
----------- case 2: 2D x 1D -> 1D
[array([-1.5659583, 1.718431 ], dtype=float32)]
----------- case 3: 2D x 0D -> 0D
[ONNXRuntimeError] : 1 : FAIL : Node () Op (MatMul) [ShapeInferenceError] Input tensors of wrong rank (0).
----------- case 4: 2D x None -> None
<class 'onnx.onnx_cpp2py_export.checker.ValidationError'> Field 'shape' of 'type' is required but missing.
[array([3.5770648, 2.8978224], dtype=float32)]
----------- end